Differential Privacy Part-II: DP Mechanisms
Having gone through the importance of differential privacy and its definition, this article motivates the theory with a practical example to make it more intuitive how the definition is applied to obtain privacy guarantees. The small town example in this previous article is just to develop an intuitive understanding of why DP would be important. In practice, for DP to be effective you would need a really large dataset such that the law of large numbers work. The law of large numbers is a law from statistics which proves that even in presence of some noisy measurements, the result of a large number of samples would converge to the true value (or very close to).
Consider the query release problem where a analyst is querying a dataset with the two queries resulting in dataset without a given row (D2) and database with the given row(D1) as defined in previous tutorial.
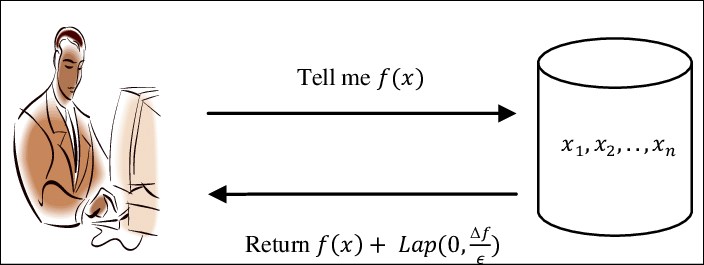
The previous tutorial defined DP as two probability distributions being close to each other by a factor of exp(epsilon). This definition is put into practice by adding noise to result of every query. The noise is sampled from a probability distribution that is calibrated according to the definition of DP. Note that the noise is added to the result of a query and not to the data itself. Since DP defines how two probability distributions vary by a factor of epsilon , we are free to sample from any probability distribution. Most popular distributions used in practice are Laplace and Gaussain.
Note: The article provides a high level overview and intuitive understanding of various mechanisms. For more comphrehensive proofs and details check out the book Algorithmic Foundations of Differential Privacy
Laplace Mechanism
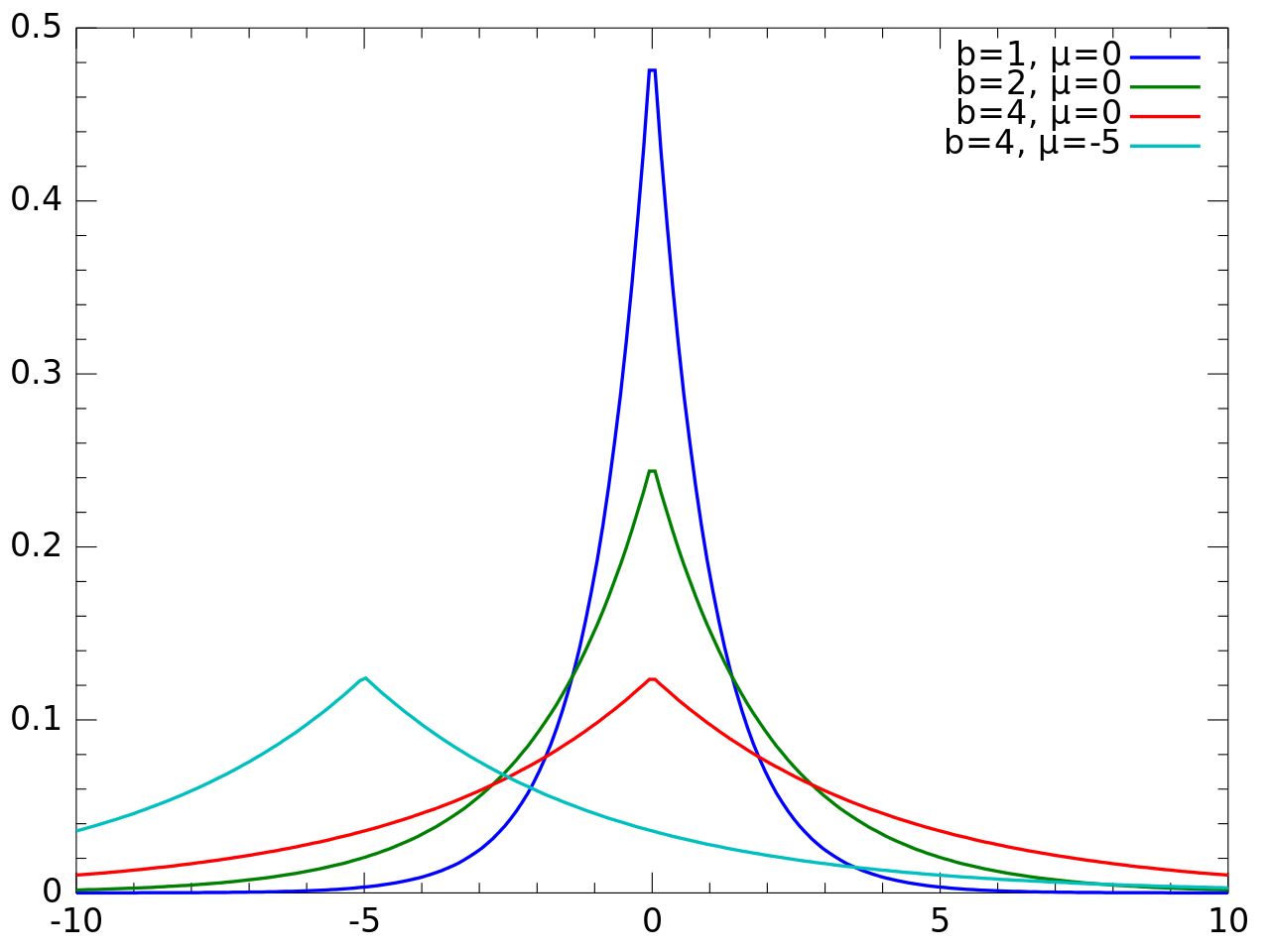
Laplace mechanism is a DP mechanism in which noise sampled from a Laplacian distribution is added to a query result. The Laplace distribution is very suitable for DP because of its sharp rise and fall for a given standard deviation.
Laplace distribution is given by
denoted by Lap(μ,b), where μ is the mean of the distribution and b is the standard deviation or scale. The Laplace noise we add is given by Lap(0,sensitivity/epsilon). This gives a privacy guarantee of DP(epsilon,0).
Below is an example of adding Laplacian noise to a counting query. A counting query is a type of query where you find the number of occurances or counts of a given data. Given that the true value is 1001. Consider two queries, the true value D1 with count 1001 and the value in which a count is dropped 1000(D2). We add Laplacian noise to both the datasets.
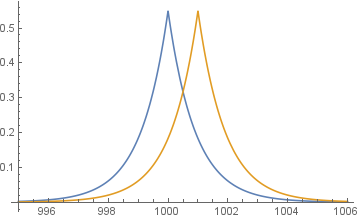
Notice that when sampled from a probability distribution, when we query with just dataset D1 and D2 if the noise added is very close at both instances, there is very little privacy guarantee. But, if both the noise are in opposite direction there is a maximal privacy guarantee. So the probability of the noises added depends on the standard deviation of the distribution we sample from. Based on the above we could develop a mechanism in which we sample for D1 and always add noise in opposite direction when D2 is queried, but we want to develop a generalized querying mechanism where we treat even differencing attacks query as the same as any other query. The adversery having a knowledge of few rows in the database wont find it hard to find out such a mechanism. Hence we rely on DP being a randomized mechanism rather than adding a fixed noise to every result of a query.
Exponential Mechanism
Exponential Mechanism can be useful when perturbation of the values by themselves could lead to drastically reduce utility. That is the privacy-utlity relationship isnt linear. Suppose a age of a person was 35 and we add noise to it the query answer is 36 or 37, the utility degrades by a factor of 1 and 2. But , there are scenerios where the utility degrades much quickly. For example, given item to be sold at price p (Assume If there are multiple people quoting same price all of them get the product) . There are three biders for 1$ 1$ and 3$. If the price is below the price p, the buyers would buy the item. Now we want to set the price p such that it makes use of the prices put by the bidder but the exact price is to be kept a secret. Suppose we add noise to $3 bidded price , it becomes 3.1$, there would 0 revenue generated. Now suppose noise is added to 1$ and it becomes $1.1, the revenue generated is $1.1 from the person who put a price of $3. But, if the price was $0.9 three people would buy the items making $2.7 revenue. From above scenerios it is evident that the utility-privacy trade off is not linear. So instead of adding noise directly to the value, we choose a value based on some criteria that accounts for the utility gained and accordingly selects a value with some randomness. The criteria for choosing the value is given by exponential mechanism.
In exponential mechanism the probability of a given choice/number is given by a scoring function exp(εu(x, r)/∆u). u is called the utility function, ∆u is the maximum change in utility (akin to sensitivity of Laplacian Noise) and ε is used to provide privacy guarantee. Depending on the set ε, we could say the mechanism is DP(ε,0) Utility is a function which gives how useful a given range of value is to a query. Exponential could be a great way to discount for utility , selecting values with higher utility and discarding values with lower utility. It also ensures when there exists values of almost equal utility the utility guarantees are still as high as possible while maintaing privacy. If two or more choices have almost the same scores they have almost equal chances of being randomly picked which sacrifices utility to a certain extent but by a small loss since score functions of both are nearly equal. But, even presence of such cases there is a privacy guarantee.
To solve the above bidding problem, we can have a range of continious values from 0.8 to 3.0 with a step of 0.1. The utility score will be the revenue generated if the item is sold for a given price. Calculate utility for all the values and find the maximum sensitivity denoted by ∆u. Further, Calculate exp(εu(x, r)/∆u) normalized by sum of exp(εu(x, r)/∆u) for all the continious values in the range, this give us a probability. The probability values generated by the mechanism is the probability with which each of the values would be selected as a result of a mechanism. Higher the epsilon, higher privacy guarantee. It would define the range within which similar values would have similar probabilities.
Composition
Composition is the property of DP which describes how the privacy guarantees hold not just over a single query but also multiple queries. It also provides mechanism to handle privacy guarantees over several queries. Simplest rule of them is basic composition, which states that if k DP algorithms are run the privacy is now DP(kε,k𝛿).
I will explain different types of composition in detail in a future article. There are various ways of handling composition over several queries.
I will put an update here when I complete writing a Part-III.